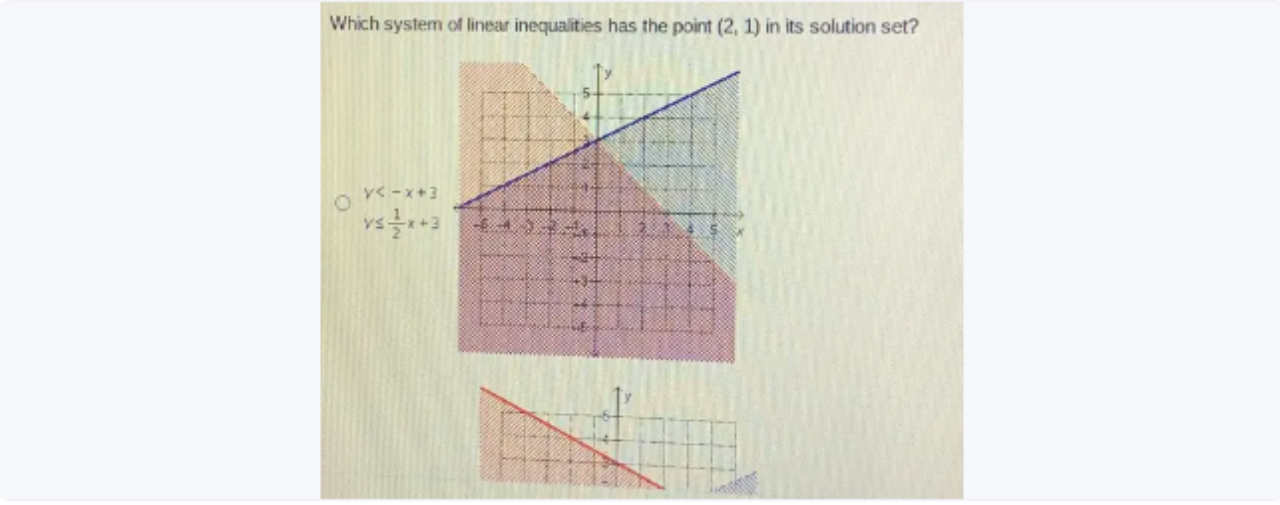
It is essential to know which system of linear inequalities contains the point (2, 1) in its solution set in order to comprehend how mathematical systems define regions of possible solutions. In mathematics, a system of linear inequalities typically consists of a number of linear inequalities that define a shaded region on a coordinate plane where all of the inequalities are satisfied simultaneously.
For point (2, 1) to be remembered for the arrangement set of such a framework, it should fulfil the circumstances forced by all imbalances inside that framework. This article demonstrates which system of linear inequalities has the point (2, 1) in its solution set? the connection between algebraic concepts and graphical representations and how linear inequalities can be used in practice to define solution spaces that are feasible.
What do you mean by a System of Linear Inequalities?
An assortment of numerous straight disparities including at least one factor is alluded to as an arrangement of direct imbalances. A straight condition with the images more prominent than (>), not exactly (), more prominent than or equivalent to (), or not exactly or equivalent to () can be utilized to address every imbalance in the framework. These inequalities taken as a whole define a region or set of points in a coordinate plane where all of these inequalities are satisfied simultaneously.
To address the arrangement set, which includes all points that satisfy the circumstances imposed by each difference, this area is frequently hidden. The fundamental mathematical concept of a system of linear inequalities is frequently used in optimization, engineering, and economics. These systems make it possible to model constraints and conditions from the real world, like limits on production, allocations of resources, or budgets.
Using GathMath for Finding the System of Linear Inequalities
Using Gauth simplifies the process of solving systems of linear inequalities by offering insights and explanations that aid in understanding complex mathematical concepts effectively and efficiently.
Step 1: Access Gauth
To begin, use the Gauth platform’s web interface or mobile app. Make sure your device is compatible with it so you can use it easily and navigate it without any problems.
Step 2: Write your Question or Upload a Picture
In the query field that is provided, clearly state your system of linear inequalities, or upload a picture that shows the inequalities involving one or more variables. Make certain that all inequalities are properly formatted in accordance with mathematical conventions.
Step 3: Wait for Processing
Submit your query or image and give Gauth time to process the data. For precise responses, the platform makes use of cutting-edge artificial intelligence (AI) algorithms that interpret visual data and analyze textual queries.
Step 4: Get your Solution
Get the processed solution from Gauth, which typically contains the linear inequalities system and the solution set, which can be displayed graphically or textually.
Step 5: Review the Solution
Carefully examine the Gauth results to ensure accuracy and comprehension of the mathematical concepts at play. Check to see if the solution set, any accompanying explanations, or visual representations, meet your expectations and the problem statement.
Benefits of Using Gauth for Homework
Gauth is an amazing AI tool for doing homework. Some of the benefits are described below.
● Instant Arrangements
Gauth gives quick solutions to a great many numerical issues, which saves understudies time and permits them to zero in additional on understanding ideas as opposed to battling with computations.
● Step-by-Step Explanations
Gauth provides detailed step-by-step explanations for each solution. Students’ comprehension and problem-solving abilities are significantly improved by this feature, which helps them comprehend the method used to solve the problem.
● Flexibility and accessibility
Gauth is accessible on a variety of devices, allowing students to access homework assistance at any time and from any location. This accessibility makes it easier to learn outside of traditional classroom hours and encourages regular practice.
● Enhanced Exactness
Using progressed calculations, Gauth guarantees exact answers for numerical issues. Students gain confidence in their homework submissions and effectively reinforce their understanding of mathematical concepts thanks to this accuracy.
Final Talk
Understanding how mathematical constraints define feasible regions in a coordinate plane requires knowing which system of linear inequalities includes the point (2, 1) in its solution set. The process is simplified and made more accessible by tools like Gauth, which provides precise solutions and insights into the connections between constraints and variables.
 Asa
Asa